
Oft stolpert man über den Begriff Öffnungswinkel, wenn es um Okulare, Objektive, ganze Teleskope oder besonders Kameras geht. Aber woher kann ein interessierter Amateur für sich selbst überhaupt wissen, was für einen Öffnungswinkel seine Instrumente haben? Dass die Ermittlung gar nicht so schwierig ist bzw. dass man mit einfachen Annäherungen bereits recht genaue Ergebnisse erzielen kann, darum soll es im heutigen Artikel gehen.
Beginnen wir mit dem typischen Fall einer Astrokamera, die im Primärfokus eines Teleskops angeschlossen ist. Primärfokus oder auch ‚prime focus‘ bedeutet, dass die Kamera direkt ohne weitere optische Elemente an das Teleskop angeschlossen wird, so dass das Teleskop wie ein Teleobjektiv funktioniert.
Das Objektiv des Teleskops erzeugt ein scharfes Bild genau im Abstand seiner Brennweite. Dieses Abbild ist nicht etwa flach, sondern minimal gekrümmt (siehe Bildfeldwölbung) und entspricht – ohne weitere optische Korrekturelemente wie etwa Flattener – einem kleinen Stück eines Kreises mit dem Radius f0. Der gesamte Kreis entspräche dabei 360° und das Abbild auf dem Chip einem kleinen Teil davon, der sich mit einer einfachen Dreisatzrechnung (ja, schwieriger wird es nicht!) berechnen lässt.
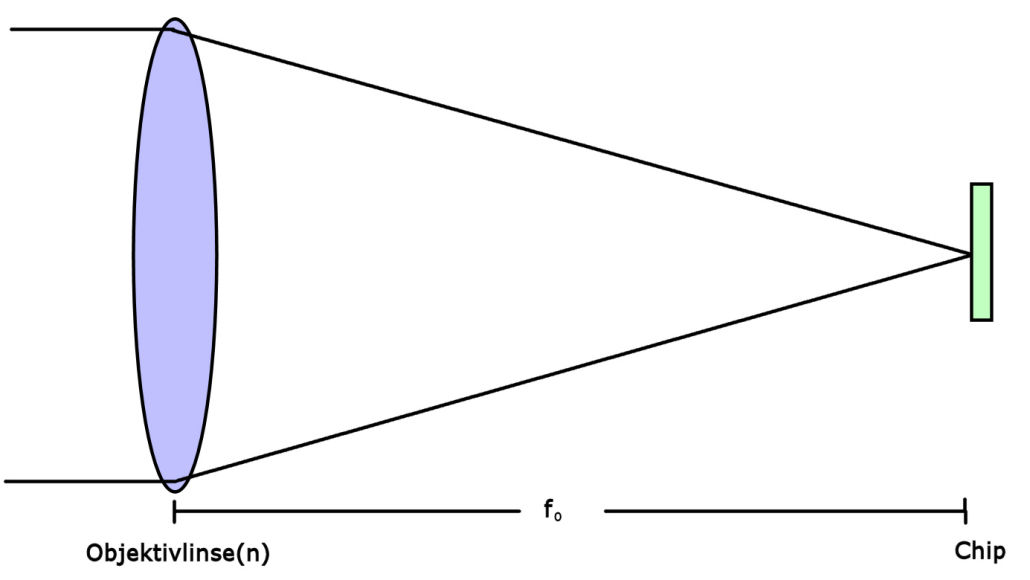
Beispiel 1: Ein Refraktor mit der Brennweite 900mm erzeugt ein scharfes Bild in 900mm Abstand. Der gesamte Umkreis in diesem Abstand hat einen Umfang von 2*π*900mm, also 5.655mm. Diese 5.655mm entsprechen 360°. Hat der Kamerachip eine Länge von 12mm, so wird darauf ein Winkelausschnitt von
12mm / 5.655mm * 360° = 0,76°
abgebildet.
Beispiel 2: Eine Vollformatkamera mit einem Chip von 24mm x 36mm sei an einem ED80-Teleskop mit 440mm Brennweite befestigt. Hier ergibt sich ein horizontaler Öffnungswinkel von etwa
36mm / 2.765mm * 360° = 4,7°
Mit dieser einfachen Formel kann man schnell errechnen, wie groß mit der gewählten Kamera und dem zu verwendenden Teleskop der resultierende Bildausschnitt ist.
Beim zweiten Fall wenden wir uns dem visuellen Eindruck am Himmel zu. Hier hängt das Ganze stark vom verwendeten Okular ab. Heutzutage wird für jedes Markenokular immer der Öffnungswinkel, der sich durch die optische Konstruktion ergibt, mit angegeben. Welchen Winkel am Himmel man damit überblicken kann, hängt dann nur noch von der gesamten Vergrößerung des Teleskops ab. Diese Vergrößerung eines Teleskops lässt sich einfach errechnen, indem man die Brennweite des Teleskops durch die Brennweite des Okulars teilt.
Beispiel 3: Am oben erwähnten Teleskop mit 900mm Brennweite befinde sich ein modernes Weitwinkelokular mit 22mm Brennweite und 82° Öffnungswinkel. Dann hat das Teleskop eine Vergrößerung von 900mm / 22mm = 41fach
Durch das Okular mit seinem Öffnungswinkel von 82° sieht man nicht 82° des echten Himmels, sondern durch die Vergrößerung nur den 41. Teil davon, also 82° / 41 = 2°. Man kann mit dieser Kombination also echte 2° am Himmel gleichzeitig im Blickfeld haben.
Beispiel 4: An einem C9.25-Spiegelteleskop mit 2.350mm Brennweite kommt nun ein 6mm Planetenokular mit 52° Gesichtsfeld zum Einsatz. Die Vergrößerung liegt also bei 2.350mm / 6mm = 392fach und der echte Blickwinkel am Himmel 52° / 392 = 0,13° oder knapp 8 Bogenminuten.
Welche Vergrößerungen überhaupt sinnvoll sind oder um was es sich bei der Austrittspupille handelt, das finden Sie dort in den entsprechenden Artikeln.




Spielt der Feldblendendurchmesser des Okulares
keine Rolle bei der Berechnung, oder ist seine
Bedeutung zu klein?
Danke für Ihre Frage! Bei der Feldblende handelt es sich um eine in das Okular eingebaute ringförmige Blende, die das Gesichtsfeld begrenzt. Bei den Okularen habe ich nur den vom Hersteller vorgegebenen gesamten Öffnungswinkel genutzt. Insofern fließt das Maß der Feldblende in die weiteren Berechnungen nicht mehr ein.