Was ist eigentlich … die Auflösung?

Oft genug fällt bei Diskussionen in Amateurkreisen oder in Foren im Zusammenhang mit den verwendeten Teleskopen der Begriff »Auflösung«. Intuitiv kann man sich darunter bereits vorstellen, dass die Auflösung ein Maß dafür ist, wie kleine Details sich mit dem Teleskop darstellen lassen. Doch gibt es in diesem Zusammenhang noch einige weitere interessante Aspekte, die ich in diesem kleinen Beitrag näher beleuchten möchte.

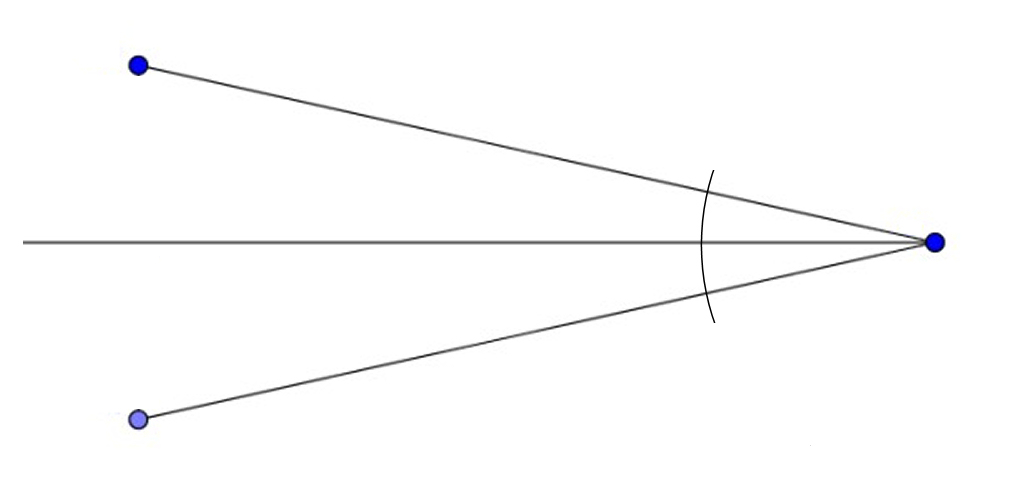
Um einen Vergleichsmaßstab bzw. eine eindeutige Referenz bei der Angabe der Auflösung zu haben, wird diese definiert als die Möglichkeit, zwei eng beieinanderstehende Objekte noch getrennt abzubilden. In der Astronomie eignen sich hierfür wunderbar Doppelsterne, die es in praktisch jedem gewünschten Abstand am Himmel zu finden gibt.

Dass ein Teleskop überhaupt eine Grenze in seiner Auflösung hat, hat etwas mit der Wellennatur des Lichtes zu tun. Entscheidend dabei ist, dass die Auflösung eines Teleskops sowohl von der Wellenlänge des Lichtes als auch vom Durchmesser der Frontlinse beim Refraktor oder vom Spiegeldurchmesser bei einem Spiegelteleskop abhängt.

Setzt man nun einfach eine mittlere Wellenlänge des Lichtes (üblicherweise Grün) voraus, so reduziert sich die Formel zur Berechnung der Auflösung in Bogensekunden auf die einfache Formel:

Auflösung_Teleskop = 138 / Objektiv_mm

Ein häufig verwendeter Teleskoptyp ist ein Newton-Teleskop mit 150mm Spiegeldurchmesser. Hier ergibt sich eine Auflösung von A = 138 / 150 = 0,92″. Ein kleines Reiseteleskop mit einem Frontlinsendurchmesser von 60mm hat dagegen nur eine Auflösung von A = 138/60 = 2,3″. Ein sehr großes Schmidt-Cassegrain-Teleskop mit einem Spiegeldurchmesser von 350mm (so zum Beispiel ein C14) hat eine theoretische Auflösung von 0,4″.

Im letzten Beispiel wurde bewusst die Formulierung »theoretische Auflösung« genutzt, um darauf hinzuweisen, dass in diesen hochauflösenden Bereichen auch noch andere Einflüsse eine starke Rolle spielen. Hierzu zählen natürlich einerseits die optische Qualität der weiteren im Teleskop verbauten Komponenten wie weitere Spiegel oder Okulare, andererseits aber auch die Begrenzung der Auflösung durch die Atmosphäre (Turbulenzen, Schlierenbildung, Jetstream…). Üblicherweise ist die Auflösung bei der visuellen Beobachtung auf ca. 1″ begrenzt und nur in seltenen Ausnahmefällen besser.

Und dennoch lohnen sich auch Teleskope mit deutlich besserer Auflösung als die eben erwähnte 1 Bogensekunde. Auch bei visueller Beobachtung kommt es immer wieder einmal zu Momenten deutlicher Luftruhe, wo einem kurzzeitig weitere Details buchäblich ins Auge fallen. Diesen Effekt macht man sich besonders bei der Fotografie von Deep-Sky-Objekten oder Planeten zunutze, indem aus einer Unmenge von Einzelaufnahmen nur die besten verwendet werden. Besonders bei der Planetenfotografie bedient man sich üblicherweise der Vidoetechnik, wo in einer Sekunde 30, 50 oder mehr Bilder aufgenommen werden und damit in ein bis zwei Minuten durchaus mehrere tausend Einzelaufnahmen zusammenkommen. Von dieser Unmenge an Einzelaufnahmen werden dann teilweise nur fünf Prozent oder weniger genutzt, die dann in der automatisch durchgeführten Überlagerung ein rauschfreies und extrem scharfes Abbild liefern.

In diesen Bereichen ist es sogar besonders wichtig, die Auflösungsgrenze seines Teleskops zu kennen. Nach ebenfalls durch die Wellennatur des Lichtes bestimmten Kriterien benötigt man zur Abbildung einer bestimmten Auflösung eine Kamera mit mindestens zwei bildaufnehmenden Pixeln pro solchem Abstand.

Am Beispiel des erwähnten C14 sieht das dann so aus: Das C14 hat eine Brennweite von 3500mm. Stellt man sich dies als Radius eines Kreises mit 360° von, so hätte dieser einen Umfang von 22.990mm. 1° wären dann der 360te Teil, also 61mm. Eine Bogenminute ist dann wiederum der 60te Teil hiervon, also ca. 1mm und eine Bodensekunde der 60te Teil von 1mm, also ca. 17µm. Ein Detail von 0,4″ (=Auflösung eines C14, s.o.) wird demnach auf etwa 7µm abgebildet. Wegen der erforderlichen zwei Pixel benötigt man also eine Kamera mit einer Pixelgröße von 3.5µm, um die theoretische Auflösung des Teleskops auch abbilden zu können.

Das menschliche Auge allein hat übrigens eine Auflösung von ca. 1 Bogenminute.